Descargar el fichero: interpolacion.xlsx
Disponemos de unos datos con los que hacemos un gráfico. Aún no siendo muchos datos Excel es capaz de realizar el gráfico de forma suavizada. ¿Cómo ha sido capaz Excel de inventarse los datos que faltan?. Ha sido algo increíble, Excel traza una curva con pocos datos y esa curva pasa exactamente por esos puntos, pero el resto de puntos se los inventa de una forma bastante adecuada, ¿cómo lo hace?. La respuesta está en la palabra: INTERPOLACIÓN.
Existen diferentes métodos para interpolar. Podemos ver lo que dice la Wikipedia para este tema. La interpolación más sencilla es la interpolación lineal.
Interpolación lineal
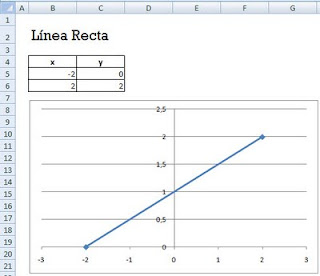
La interpolación lineal parte de dos puntos y pretende establecer la línea recta que pasa por ambos puntos. De esta forma podremos determinar los puntos intermedios entre ambos puntos como los puntos que pertenecen a esa recta.
La ecuación de la recta es:
y=a+bx
siendo
- y la variable dependiente. Se representa en el eje de ordenadas, en vertical
- x la variable independiente. Se representa en el eje de abcisas, en horizontal
- a la constante de la recta. Es el punto de corte con el eje y
- b la pendiente de la recta
Si únicamente disponemos de dos puntos (dos parejas de datos (x,y)) podemos calcular la recta de regresión y habremos obtenido una recta que pasa exactamente por esos dos puntos. Esa recta es la misma que hubiéramos obtenido si buscamos la recta de interpolación. Por tanto, en el caso de una recta, es lo mismo interpolar que ajustar por mínimos cuadrados cuando únicamente disponemos de dos puntos. La recta pasa justo por esos dos puntos y la correlación es perfecta, siendo R2 igual a 1.
Esto lo podemos ver en la Hoja1 de nuestro fichero.
Hemos representado la recta utilizando los gráficos de tipo dispersión con líneas suavizadas y marcadores.
Sobre la recta obtenida hemos añadido una línea de tendencia.
La ventana que se abre nos permite añadir diferente líneas de tendencia:
- Exponencial
- Lineal
- Logarítmica
- Polinómica
- Potencial
- Media móvil
Elegiremos, para este caso, la lineal y al final de la ventana marcaremos las opciones:
- Presentar ecuación en el gráfico
- Presentar el valor R cuadrado en el gráfico
Observamos que R2 es igual a 1 y que la ecuación de la recta es:
y=0,5x+1
Al tratarse únicamente de dos puntos en la nube de datos la recta pasa exactamente por ellos y el ajuste es perfecto (R2=1).
La ecuación de la recta se puede obtener con la siguientes funciones estadísticas.
- a es la constante =INTERSECCION.EJE(conocido_y;conocido_x)
- b es la pendiente =PENDIENTE(conocido_y;conocido_x)
Aunque estamos hablando de interpolación se ha de considerar que no estamos aplicando los clásicos métodos de interpolación. Lo que hacemos es efectuar un ajuste por el método de los mínimos cuadrados a una nube de datos que únicamente tiene dos puntos, por lo que necesariamente la recta de regresión que obtenemos pasa por esos dos puntos. Siendo la correlación perfecta podemos inferir que la recta de regresión coincide con la recta que obtendríamos mediante los métodos de interpolación lineal.
Interpolación Parabólica
Una parábola es un polinomio de grado 2, cuya ecuación es:
y=a+bx+cx2
En la Hoja2 de nuestro fichero podemos ver un caso en el que nos dan 3 puntos. Nuestra nube de puntos es pequeña y lo que pretendemos es encontrar la parábola que pasa justo por esos tres puntos. Si lo conseguimos habremos obtenido una interpolación parabólica.
Pulsando con el botón derecho del ratón sobre el gráfico (justo sobre la curva) obtenemos el menú contextual y elegimos Agregar línea de tendencia.
También marcamos abajo las opciones:
Así veremos la ecuación de la parábola:
y también veremos el coeficiente de determinación que es R2=1, lo cual indica que estamos en un caso de correlación perfecta.
Observar que aunque aumentemos el grado del polinomio (lo que aquí Excel llama 'Ordenación') no por ello mejora el valor de R2 ya que lo máximo que puede valer es 1.
La sorpresa es que al trazar Excel la parábola (línea negra) no coincide con la curva (línea azul), y ambas curvas pasan por los tres puntos. La respuesta es que existen muchas formas de interpolar y por lo que vemos Excel en la curva azul ha elegido otro método muy diferente del que nosotros estamos buscando. Nosotros queríamos una parábola y usando este sistema hemos obtenido la parábola, que es un polinomio de grado 2.
Para calcular la ecuación de la parábola debemos determinar los valores de sus parámetros: a, b y c. Nos reservamos el método para más adelante, ya que lo aplicaremos para un caso de un polinomio de grado 4 y como es un método matricial es válido para cualquier grado.
A la vista del gráfico podemos observar la ecuación de la parábola:
Pulsando con el botón derecho del ratón sobre el gráfico (justo sobre la curva) obtenemos el menú contextual y elegimos Agregar línea de tendencia.
También marcamos abajo las opciones:
- Presentar ecuación en el gráfico
- Presentar el valor R cuadrado en el gráfico
Así veremos la ecuación de la parábola:
y también veremos el coeficiente de determinación que es R2=1, lo cual indica que estamos en un caso de correlación perfecta.
Observar que aunque aumentemos el grado del polinomio (lo que aquí Excel llama 'Ordenación') no por ello mejora el valor de R2 ya que lo máximo que puede valer es 1.
La sorpresa es que al trazar Excel la parábola (línea negra) no coincide con la curva (línea azul), y ambas curvas pasan por los tres puntos. La respuesta es que existen muchas formas de interpolar y por lo que vemos Excel en la curva azul ha elegido otro método muy diferente del que nosotros estamos buscando. Nosotros queríamos una parábola y usando este sistema hemos obtenido la parábola, que es un polinomio de grado 2.
Si aumentamos el grado del polinomio en la ventana de las opciones de la línea de tendencia no cambia la curva ajustada y no mejora R2 ya que al llegar a 1 ha llegado al máximo. R2 igual a 1 indica que estamos ante un ajuste perfecto por lo que no se gana nada intentando aumentar el grado del polinomio.
Para calcular la ecuación de la parábola debemos determinar los valores de sus parámetros: a, b y c. Nos reservamos el método para más adelante, ya que lo aplicaremos para un caso de un polinomio de grado 4 y como es un método matricial es válido para cualquier grado.
A la vista del gráfico podemos observar la ecuación de la parábola:
y=a+bx+cx2en nuestro caso es: y=1+0,5x-2x2
En la Hoja3 de nuestro fichero pretendemos obtener el polinomio de interpolación que pasa por 4 parejas de datos.
La curva que obtenemos es la siguiente.
Nuevamente, observamos que pese a estar en el caso de correlación perfecta (R2=1) nuestro polinomio de grado 3 (color negro) no coincide con la curva del gráfico generada por Excel (color azul).
Polinomio grado 4
En la Hoja4 disponemos de 5 parejas de datos, con lo que podemos obtener un polinomio de grado 4.
Aquí también R2=1 ya que el polinomio pasa por todos los puntos.
Interpolación: determinación de la curva
En la Hoja5 vamos a estudiar un caso real. Nos proporcionan datos para construir dos curvas.
Por cada curva son cinco parejas de datos, por lo que el polinomio al que queremos llegar es de grado 4. Siempre el grado del polinomio es uno menos que el número de parejas de datos. Esto se debe a que para determinar un polinomio de grado 4 necesitamos determinar 5 parámetros:
y=a+bx+cx2+dx3+ex4
Los cinco parámetros a determinar son: a, b, c, d, e.
En lugar de usar esta terminología vamos a denotar a los parámetros así: a0, a1, a2, a3, a4, a5.
Por tanto el polinomio de grado 4 será este:
y=a0+a1x+a2x2+a3x3+a4x4
Esta expresión se puede escribir de forma matricial y así es válida no solo para polinomios de grado 4 sino para polinomios de cualquier grado.
y=AX
Siendo A un vector fila con todos los parámetros del polinomio:
a0, a1, a2, a3, a4, ......, an.
Siendo X un vector columna con la variable x elevada a los diferentes grados:
x0, x1, x2, x3, x4, ......, xn.
Excel dispone de una función matricial que calcula todos los parámetros del vector A. La función que emplearemos es la siguiente:
{=+ESTIMACION.LINEAL(y;x^{1;2;3;4})}
Hemos añadido las llaves {} para indicar que es una función matricial, pero no debemos escribir nosotros esas llaves, ya que es Excel el que las pone al validar con CONTROL + MAYÚSCULAS + ENTER.
Creamos una tabla para la Curva 1. En la zona amarilla escribimos nuestra función matricial.
=+ESTIMACION.LINEAL(Curva1;X^{1;2;3;4})
Previamente hemos nombrado los siguientes rangos.
Para la Curva 2 construimos una tabla similar.
En las celdas amarillas de esta segunda tabla escribimos la siguiente fórmula matricial:
=+ESTIMACION.LINEAL(Curva2;X^{1;2;3;4})
Los valores interpolados son los dados por la siguiente tabla. Establecemos el valor de x (color verde) y luego con SUMAPRODUCTO calculamos el valor y interpolado para cada curva.
Lo que estamos haciendo es una regresión múltiple donde las variables que usamos las hemos transformado para que sean los diferentes valores de la variable x elevados al grado necesario.
La correlación es perfecta. Se puede comprobar dando valores a x en la celda J20 y viendo que para los valores de la tabla original de datos los valores interpolados que se obtienen son los mismos que los de la tabla de datos.
Práctica
Usando este método puede intentar obtener el polinomio de grado 4 que interpola los datos de la Hoja4. Puede comprobar si lo ha realizado correctamente ya que en el gráfico se ve la ecuación del polinomio a la que ha de llegar.
Obtendrá los siguientes valores.
y=1+0,5x-2x2+0,3x3+0,2x4
Para facilitar el cálculo hemos dejado la tabla preparada con sus nombres de rango creados.
Falta introducir la fórmula matricial ESTIMACION.LINEAL que ha de introducirse en las celdas amarillas del rango E5:I5.
Para introducir una fórmula matricial ha de seguir tres pasos.
ESTIMACION.LINEAL es una fórmula matricial.
Como toda fórmula matricial requiere 3 pasos:
1. Seleccionar la zona amarilla (rango E5:I5)
2. Escibir la fórmula matricial
=+ESTIMACION.LINEAL(miY;miX^{1;2;3;4})
3. No pulse ENTER para validar.
Debe pulsar las 3 teclas siguientes:
CONTROL + MAYUSCULAS + ENTER





























las lineas de tendencia de los gráficos consideran todos los puntos disponibles.
ResponderEliminarPero al dibujar las rectas suavizadas, Excel utiliza Splines, que consideran para cada punto el anterior y el posterior, no todos los puntos. se trataría de una interpolación localizada alrededor de cada punto.
Hola PacoMegia.
ResponderEliminarGracias por tu comentario, aporta luz sobre el modo en que Excel suaviza las curvas.
El enlace de la Wikipedia que explica esto está en:
http://es.wikipedia.org/wiki/Spline
Hola Adolfo, la verdad es que es muy útil para ahorrarnos tiempo en algunos casos en mi trabajo. Así que me gustaría que me resolvieras mi duda. He intentado reproducir lo que has hecho en la hoja 5, y cuando meto las fórmulas matriciales (la de estimacion.lineal) en las cinco celdas contiguas, me da siempre el mismo valor. Y no culpo a Excel de esto, ya que la fórmula es exactamente la misma en las cinco celdas, pero sé que está mal ya que estamos operando con matrices. Igual me tengo que empollar el uso de matrices en excel, pero no sé si me puedes decir en qué estoy fallando.
ResponderEliminarGracias,
Miguel Ángel
Bueno, tengo otra duda, ¿hay límite en el grado del polinomio?
ResponderEliminarGracias,
Miguel Ángel
Hola Miguel.
ResponderEliminarUna fórmula matricial requiere tres pasos:
1. Seleccionar la celdas conde la fórmula matricial dejará sus resultados
2. Escribir la fórmula matricial
3. Para validar no pulses Enter. Se deben pulsar simultáneamente:
CONTROL+MAYUSCULAS+ENTER
Normalmente fallamos en pulsar las tres teclas en la forma correcta. Pulsa primero la tecla CONTROL, y sin soltar, pulsa la tecla de las MAYUSCULAS (no la de bloqueo mayúsculas, sino el Shift), y sin soltar ninguna de las teclas anteriores, pulsa finalmente la tecla ENTER.
En la Práctica propuesta se dan los resultados que deben salir. Prueba con esos datos. Te debería salir.
Respecto al grado del polinomio que esto soporta no sabría decirte. Pruébalo a ver que tal aguanta.
Un saludo.
Hola Adolfo,
ResponderEliminarde los tres primeros pasos que comentas, ¿puedes explicarme el primer paso?, igual ahí es donde fallo. Porque si veo las llaves al final, supongo que es que el tercer paso lo hago bien.
Si me sale, te prometo decirte hasta qué grado consigo usarlo. Incluso intentaré usando un loop, que una macro me organice eso para que todas las veces que lo use, con diferente número de puntos, sea lo más rápido posible.
Gracias,
Miguel Ángel
Hola Miguel.
ResponderEliminarHe dejado preparada la Hoja4 con una tabla para introducir la fórmula matricial. Baja nuevamente el fichero para verlo.
El primer paso consiste en señalar con el ratón las celdas amarillas del rango E5:I5.
Espero que ahora te funcione.
Un cordial saludo.
Hola Adolfo,
ResponderEliminarEso era lo que no sabía. Muchas gracias, ya te cuento qué consigo.
Miguel Ángel.
Hola Adolfo,
ResponderEliminarYa sé usar esa utilidad. Gracias.
Mi gozo en un pozo, sólo sirve hasta grado 16. Debo de ser un poco bruto.
Muchas gracias por todo,
Miguel Ángel.
Hola que tal. Queria hacerte una consulta. Quiero saber si excel utiliza en las curvas suavizadas entre puntos splines u otro tipo de interpolación. O si utiliza splines pero no cubicas, quizas cuadraticas, porque he calculados las curvas splines cubicas y no coinciden con las que excel me grafica como linea suavizada. Revise los calculos mios y estan bien. Por suerte no es complicado armar las splines. Bueno, muchas gracias. Saludos.
ResponderEliminarhola Adolfo, genial tu explicación. ya lo voy a probar. sabes, quisiera ver si me puedes ayudar con otra inquietud que no va mucho con el tema.
ResponderEliminarmira, tengo un grupo de datos los cuales gráfico, y les voy probando lineas de tendencia, las cuales la que mas me gusta es la logarítmica, es la que menos R2 me da y mis datos se ajustan perfecto a su forma. la cosa va, en como puedo obtener los "estadísticos" (asi como los de la regresión lineal que tiene por default en las herramientas excel) ya que me interesa bastante esta forma y necesito su error típico para proyectar con bandas (optimista, pesimista) los resultados.
saludos
Pedro
Hombre para agradecerte, es ya la tercera vez que tu blog me aclara una duda... Entre ayer y hoy :). Estaba un poco atareado entonces hasta ahora tengo la oportunidad de darte las gracias. Muy buen blog util, claro y conciso.
ResponderEliminarSaludos desde Colombia.
Adolfo, quiero felicitarte por esta nota. Era lo que estaba buscando desde hace tiempo, pues requería hallar los coeficientes de una ecuación cuadrática, usando una función. Tengo una pregunta.
ResponderEliminarSi tengo la siguiente ecuación
y=0,000304213X^2+0,021927382X-0,081761667
Es posible despejar con formulación, el valor de x a partir de un valor de y conocido?.
¿Tiene alguna implicación matemática intercambiar los argumentos (y) conocido, (x) conocido de la función estimación.lineal?. Esto con el fin de evitarme el hecho de tener que despejar x
De nuevo gracias por la nota.
Hola Mauricio.
ResponderEliminarPuedes despejar x perfectamente ya que se trata de una ecuación cuadrática. Puedes consultarlo en este enlace la del Wikipedia:
Ecuación de segundo grado
Si existe una diferencia entre hacer un análisis de regresión de Y frente a X, o de X frente a Y. Las diferencias en el coeficiente de determinación R^2 no son enormes pero existen.
Al calcular la recta de regresión por el método de los mínimos cuadrados, lo que se hace es minimizar la distancia entre el valor de Y real y el Y de la recta. Esto significa que lo que se pretende minimizar son las distancias en VERTICAL entre el punto real y el predicho por la recta. Si cambias las variables, dándolas la vuelta, lo que harías es minimiar las distancias en HORIZONTAL. No existe una gran diferencia entre ambos sistemas de minimización pero la recta ques e obtiene difiere ligeramente y el coeficiente de determinación también.
Un cordial saludo.
HOLA SR ADOLFO APARICIO COMO ESTAS?
ResponderEliminarBUENO ESPERO QUE BIEN....BUENO MI CONSULTA ES COMO PUEO PROGRAMAR LA SUMA CONDICIONAL (SUMAR.SI O SUMAR.SI.CONJUNTO) EN UNA MACRO...BUENO SIN MAS DECIRLE ESPERO SU RESPUESTA EN EL BLOG Y GRACIAS POR EL GRAN APORTE QUE HACE A LA COMUNIDAD MEDIANTE EL BLOG
Hola, he conseguido la función matricial. Mi pregunta es:
ResponderEliminar¿Cómo puedo representarla?
Buenas Adolfo.
ResponderEliminarMuchas gracias por este documento, mes esta siendo de gran ayuda. Mi pregunta es:
-Como puedo calcular los coeficientes de la interpolació potencial a partir de una serie de datos?
Gracias
Hola!
ResponderEliminarMuy buena la publicación. Me gustaría saber qué tipo de interpolación hace excel cuando seleccionamos la opción de gráfico con disperción con lineas suavizadas (obviamente para una serie de datos que no coincide con ninguna de las predeterminadas).
Estoy probando con una serie y se forman curvas suaves pero no logro pillar esta información.
Saludos y muchas gracias!
Mi pregunta tiene que ver con la interpolación pero es más de estadística. Estoy intentando establecer una recta de regresión (en principio lineal)entre los datos de temperatura media de dos estaciones meteorologicas proximas, con objeto de estimar datos perdidos de una estación a partir de los de la otra. El nº de datos es alto: N=2500. Si utilizo r2 como criterio de ajuste, observo que la R2 puede ser más alta cuando tomo una parte de los datos (p.e. 500) que cuando utilizo todos (2500). Además la R2 de 500 datos varía dependiendo del tramo de datos que elija. ¿que recta de regresión debería usar como ecuación de interpolación: la que me proporciona todo el conjunto de datos o la de una parte de ellos que proporciona una r2 más alta?¿existe algún método estadístico que me permita elegir la mejor ecuación (o modelo), con parte o todos los datos, de una forma automática y robusta?
ResponderEliminarGracias por tu dedicación.
Y en el caso de la curva "s" cual sería la formulación de interpolación?
ResponderEliminarHola. He utilizado el método de obtener la ecuación de la curva. La ecuación si que la consigo, pero he comprobado si es correcta la ecuación que me da excel con la que tenia y no es se parecen. Para la comprobación he introducido un valor conocido "X", pero la "Y" resultante sale muy diferente.
ResponderEliminar¿cuál puede ser el error? o como puedo solucionarlo?
Hola a todos, voy a exponer un problema que se me ha planteado por si alguien conoce una solución. Dispongo de parejas de valores tensión y deformación que he obtenido en una ensayo de carga. Excel me ha generado dicha curva. Ahora requiero conocer el valor de deformación asociado a cargas que no he probado en campo, pero que al tener la gráfica que genera Excel me pregunto si ya podría obtener dichos valores. Es decir, establecer para un cierto valor del eje X cuál es el valor de Y asociado a la gráfica representada. Espero haberme explicado con la suficiente claridad. Muchas gracias.
ResponderEliminarHola. Muy buena la enseñanza Gracias Adolfo. Una pregunta, en la interpolación lineal como consigo el error del resultado.
ResponderEliminarComo puedo interpolar una lista de puntos con un polinomio de grado mayor a 6 ?, ya que en el excel solo se puede hasta 6
ResponderEliminarHola Jesus.
EliminarPuedes utilizar alguno de los métodos clásicos de interpolación, por ejemplo, el método de Newton. Por Internet tiene infinidad de sitios que te cuentan este método.
Luego, puedes utilizar Excel para efectuar los cálculos.
Un saludo.
HOLA ADOLFO, COMO PODRÍA HACER UNA EXTRAPOLACIÓN DE UNA CURVA DE GRADO 6?
ResponderEliminarHola Jacobo.
EliminarPara interpolar curvas de un grado mayor de lo que soporta Excel puedes utilizar alguno de los métodos clásicos de interpolación, por ejemplo, el método de Newton.
http://es.wikipedia.org/wiki/Interpolaci%C3%B3n_polin%C3%B3mica
Luego, puedes utilizar Excel para efectuar los cálculos.
Un saludo.
Hola Adolfo, ¿Cuál es el algoritmo para suavizar las líneas de una distribución?
ResponderEliminarHola Adolfo, gracias a las explicaciones claras y con ejemplos me he atrevido a realizar interpolaciones utilizando polinomios de orden 6. Probablemente podré reducir el grado.
ResponderEliminarEstoy realizando las interpolaciones/imputaciones sobre los datos ausentes que tengo en mi base de datos: 170 empresas, con datos/registros de 14 años (2000 a 2013) para 75 variables diferentes (como ventas ó número de empleados..).
El problema es que los datos ausentes no tienen un patron definido, a veces falta el dato de los dos primeros años, a veces un dato intermedio..muchas veces ninguno.
Trato de automatizar la función LINEST, donde debo poner los datos de las x's conocidos y los datos de las y's conocidos.
** He tratado de poner los rangos compuestos, tipo (A1:A3, A5:A14) si faltara el dato en A4, pero no funciona.
** He buscado una función anidada a LINEST que me cribe/no tenga en cuenta las casillas que contengan cero (ausente) pero no se cual.
** Por último estoy intentándolo con VBA pero de momento no me sale nada.
Te agradecería mucho si pudieras decirme por donde debería seguir.
Un saludo,
Hola de nuevo, Adolfo, he encontrado una solución. No es elegante, pero me funciona.
EliminarHe utilizado un contador, como el del video de "BUSCARV valores repetitivos", pero en lugar de buscar a un comercial he buscado las ventas/variable que fueran mayores de cero (datos no ausentes) y otro contador para las ventas/variable igual a cero (datos ausentes).
En cada tabla he puesto los datos con SI.ERROR/IFERROR( BUSCARV/VLOOKUP....(tengo mi versión excel en inglés)
Gracias a los rangos dinamicos (de nuevo gracias por el video sobre los rangos y graficos dinámicos) he podido en la primera tabla calcular el polinomio de orden 6, y en la segunda tabla interpolar/imputar.
Por ultimo, como se trata de datos con años (del 2000 al 2013) los he vuelto a reunir en una sola tabla, ordenados con BUSCARV/VLOOKUP.
Solo me queda con VBA hacer un bucle del tipo "FOR RowStarting = 3 To 2383 Step 14" porque utilizo para avanzar "Cells(RowStarting,Column)" , tengo 2383 registros/lineas y los datos van de 14 en 14 (los años). Esto ultimo no lo he terminado pero me funciona esa misma subrutina para la otra imputación/interpolación que tengo hecha mediante una especie de doble alisado exponencial (utilizando la función tendencia/TREND con un coeficiente "b", y los datos más cercanos a los ausentes con el coeficiente (1-b)).
Gracias Adolfo por compartir tus conocimientos, y por ser tan bueno explicando.
Un saludo a todos,
Bonas tardes, necesitaría su ayuda, ya que necesito saber como interpolar una gráfica exponencial!
ResponderEliminarMuchas gracias
Este comentario ha sido eliminado por el autor.
ResponderEliminarHola,
ResponderEliminarCómo puedo interpolar los datos de dos curvas similares (una está sobre la otra) para sacar sólo una línea de tendencia? Existe. una función en excel para hacer esto?
Hasta el momento he sacado promedios entre pares de datos, pero se hace bastante tedioso ya que en algunos tramos es discontinuo. Lo otro que probé es sacar 2 líneas de tendencia(una para cada curva) para obtener una tercera curva (promedio de las otras). Ambas vías son tediosas, y ando en busca de una función de excel que lo haga pero aún no la encuentro...
Buenas noches profesor Adolfo Aparicio, Felicitaciones por tus excelentes enseñanzas, las cuales me han permitido desarrollar actividades laborales y académicas de gran calidad y agilidad en los tiempos de entrega de los mismos, Gracias y muy agradecido por tus enseñanzas.
ResponderEliminarProfesor en un gráfico de dispersión en Excel se puede determinar, con una formula o por formato del gráfico ¿ cuál es el punto exacto donde e interceptan los valores de X, y de Y? La pregunta es por que estoy calculando la TIR por el método gráfico, y quiero que el gráfico se muestre solo la tasa de actualización (TIR Y Valor presente neto=0)
islande Carrillo Gallo
muy buen aporte mi estimado amigo, yo he buscado un montos de paginas que me ayuden y la solucion lo encontre en tu posto un 10/10
ResponderEliminarExcelente explicación!! Muy detallada y sobretodo, clara. Quisiera saber cómo se podría graficar (si es que se puede en Excel) las curvas de confianza para la línea de tendencia generada. Gracias!
ResponderEliminarExcelente explicación!! Muy detallada y sobretodo, clara. Quisiera saber cómo se podría graficar (si es que se puede en Excel) las curvas de confianza para la línea de tendencia generada. Gracias!
ResponderEliminarpor favor alguien de buen corazón que me ayude porque no puedo hacer
ResponderEliminarhola, no me deja bajar el fichero adjunto, lo podrias resubir por favor
ResponderEliminargracias!!
ResponderEliminarbuenas, quisiera comentar un problemita que estoy teniendo por si a alguien le paso.
ResponderEliminarEl hecho es que el polinómio que me genera excel visualmente es correcto pero la expresión matemática es erronea, basta con realizar el plot para los puntos (0,0) y (1,1) para que cuando le pido que me devuelva el polinomio que mejor se ajusta me dibuja la recta perfecta pero la expresión es y=x-1 la cual está mal. debería ser y=x.
Agradezco cualquier ayuda.
saludos
Hola, buenos días
ResponderEliminarMuchas gracias por los conocimientos.
Seria posible utilizar esto, pero en lugar de calcular valores a futuro, para calcular valores a pasado
MUCHAS GRACIAS.
ResponderEliminarMuchas gracias Adolfo, con tu explicación resolví un tema urgente del trabajo. Te debo la vida :D
ResponderEliminarHola, quisiera saber si hay modo de pasar a una celda los valores que da la ecuación. Determino una gráfica de tipo exponencial, le pido que me despliegue la ecuación en la gráfica, pero quisiera usar las constantes o valores que me da en la ecuación para reproducir de manera automática los valores del comportamiento en otra gráfica o continuar con una proyección de la curva usando esa ecuación. Saludos y de antemano gracias
ResponderEliminarHola buen día, disculpe profesor Adolfo, quisiera saber si hay un modo de actualizar la formula =+ESTIMACION.LINEAL....etc.
ResponderEliminarpor ejemplo tengo un rango de A5:A10,B5:B10, pero tras un filtro recorro 2 números y queda A5:A8,B5:B8. como puedo actualizar automaticamente la ecuación de la linea de tendencia
gracias, buen día.