Descargar el fichero: poisson.xlsm
Poisson es el nombre de una distribución de probabilidad que debe su nombre al matemático francés Siméon Denis Poisson. La distribución de Poisson o de los casos raros es una distribución de probabilidad discreta, de un único parámetro (la media), denotado por la letra griega lambda (λ). Se utiliza para estudiar las llamadas telefónicas a una centralita, los siniestros de ciertos seguros no vida, como el de incendios, y nosotros la vamos a utilizar para determinar el número de clientes que se acercan por un concesionario de coches.
Hoja1
En la Hoja 1 utilizamos la función dada por Excel
=POISSON(x;media;acumulado)
donde x es el número de sucesos.
Veamos un ejemplo:
=POISSON(2;3;0)
Estamos ante una distribución de Poisson de media 3 (λ=3). Supongamos que se trata del número de incendios que se dan en una ciudad pequeña en un mes. Por término medio, en esta ciudad se producen 3 incendios al mes.
En la expresión anterior x=2. Indica que deseamos saber cual es la probabilidad de que en esa ciudad el número de incencios en un mes sea exactamente 2. Al calcularlo obtenemos que el valor que nos da Excel es de 0,224041808. Este valor expresado en porcentaje, indica que existe una probabilidad del 22,40% de que en esa ciudad se produzcan exactamente 2 incendios en un mes.
Excel también nos proporciona la probabilidad acumulada. Para ello debemos poner en el tercer argumento de la función en lugar de un cero, un uno. Así:
=POISSON(2;3;1)
que indica la probabilidad de que en esa ciudad se produzcan en un mes, cero incendios o un incendio o dos incendios. Dicho de otra forma, nos indica la probabilidad de que se produzcan dos o menos incendios en un mes.
El valor que se obtiene es: 0,423190081 que es la suma de
POISSON(2;3;1) = POISSON(0;3;0) + POISSON(1;3;0) + POISSON(2;3;0)
0,423190081 = 0,049787068 + 0,149361205 + 0,224041808
La distribución de Poisson no es simétrica (ver gráficas), pero a medida que aumenta su media se hace más simétrica y se va pareciendo más a una distribución normal, a la que tiende en el infinito.
En un post posterior hemos incluido el método 3 y el método 4 que utilizan funciones definidas por el usuario. Hemos programado dos formas de calcular la Poisson. Ver el siguiente Post:
Programar la función que nos da una distribución de Poisson
Hoja2
En esta hoja vamos a generar un gráfico que se mueva al pulsar el usuario sobre una barra de desplazamiento. Pulse sobre los extremos de la barra de desplazamiento. Hágalo lentamente para dejar tiempo a que se refresque el gráfico. Verá cómo cambia la curva de la distribución de la Poisson.
Si tiene curiosidad en ver cómo se ha construido este sistema dinámico mire la columna Y que genera el gráfico con la función =INDIRECTO.
Hoja3
En esta hoja, simplemente, construimos dos tablas de la Poisson una sin acumular y la otra acumulada. La función acumulada se denomina Función de Distribución F(x) y la función sin acumular se denomina función de cuantía, por tratarse de una función discreta. Si fuera una distribución contínua se denominaría función de densidad.
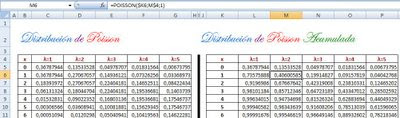
Hoja4
En la Hoja 4 construimos la POISSON INVERSA, que no existe dentro de las fórmulas de Excel.
Para ello creamos la tabla amarilla sobre una Poisson acumulada de lambda 10. Observe cómo las dos columnas de la tabla amarilla estan aparentemente cambiadas de orden. Se ha elegido precisamente este orden de las columnas para luego poder usar la función =BUSCARV. Ya que buscamos la probabilidad acumulada que se corresponde con ese número de sucesos (x). Esto se hace con la función:
=BUSCARV(ALEATORIO();tabla;2)
donde tabla es la tabla amarilla.
Así es como se construye la tabla de la izquierda, que nos da valores de la Poisson Inversa. Esto puede resultar interesante para simular sucesos. Por ejemplo, supongamos que una agencia de mensajería recibe un cierto número de encargos por minuto, que pueden caracterizarse por una Poisson de media 10. Si esto fuera así, en la columna C tendríamos una simulación de los encargos que se reciben en los sucesivos minutos.
Hoja5
En la Hoja5 afrontamos un proyecto de SIMULACIÓN donde podemos aplicar la Poisson Inversa. Supongamos que se trata de un concesionario de coches que dispone de un establecimiento comercial donde ofrece a la venta autos nuevos.
En la columan E creamos una serie de días hasta 250, que son los que el establecimiento esta abierto al público durante un año. Por cada día simulamos el número de personas que entran al comercio a preguntar por algún coche en particular (columna F). Esta simulación se realiza con la Poisson Inversa creada en las columnas B y C.
De entre los clientes interesados un cierto porcentaje llegan a realizar la compra (columna G). Este porcentaje se establece según una distribución uniforme ente el 10 y el 30% de éxito. Y redondeando hemos llegado a determinar el número de autos que se venden cada día (columna H).
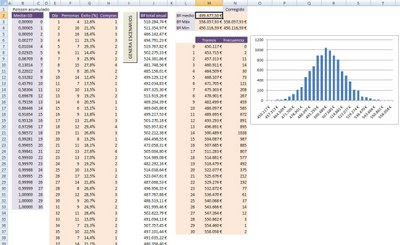
La columna H nos da los coches que se compran durante todos los días de un año concreto. Ahora se trata de realizar un elevado número de iteraciones, por ejemplo, mil. Cada una de estas mil iteraciones representaría las concrecciones, que mediante simulación, obtenemos durante mil hipotéticos años. Esta simulación la realizamos lanzando una macro y el beneficio obtenido se anota en la columna J. Cada una de las celdas de la columan J representa el beneficio que se obtendía en un año concreto de entre esos mil que hemos simulado.
Con los datos de la columna J realizamos un análisis de frecuencias, que finalmente representamos mediante un histograma. Se puede ver en este éste post la explicación de cómo se realiza un HISTOGRAMA.
El beneficio medio nos daría la mejor estimación del beneficio dado por la simulación. Cuantos más iteraciones realicemos mas estable será el beneficio estimado.
Macro
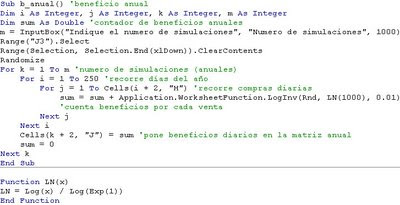
La macro que permite realizar las iteraciones de la simulación se realiza con tres FOR...NEXT concatenados. El primer bucle recorre las iteraciones que el usuario indique. Si son mil, recorrerá mil veces el bucle, una por cada año simulado. Estaríamos simulando mil años. El segundo bucle recorre los días del año (250 días). Y el tercer bucle recorre las ventas de autos realizadas cada día. Por ejemplo, si en un día se venden 3 autos, el bucle recorrera la variable j para que tome los valores 1, 2 y 3.
Por cada auto vendido estima los beneficios que el concesionario obtiene con esa venta. Esto se hace mediante una distribución LOGNORMAL, de media 1000 y desviación 0,01.
Application.WorksheetFunction.LogInv(Rnd, LN(1000), 0.01)
Supongamos que deseamos estimar aproximadamente el beneficio medio que debería obtener la simulación. Podríamos hacer el siguiete cálculo:
Por témino medio, pasan al concesionario a preguntar 10 personas al día. De los cuales, ente el 10% y el 30% de las operaciones tienen éxito. Esto supone una media del 20% de éxitos. Por tanto, el 20% de 10, son 2 ventas exitosas al día, de media. Por cada venta, el beneficio medio es de 1.000 euros. Por tanto, si realizo 2 ventas diarias en promedio, son 250 días al año, y gano 1.000 € de media. Lo que obtengo son: 2*250*1.000 = 500.000 € de beneficio medio estimado. Si realizamos las simulaciones veremos que la celda M2, que me da el beneficio medio de la simulación, se encuentra muy cercana a esos 500.000 € de beneficio medio.
En este caso, ha sido muy sencillo realizar este cálculo aproximado, pero en general tendremos que utilizar la simulación para realizar las estimaciones ya que la complejidad de los problemas dificultan o impiden estos cálculos.
Código:
Sub b_anual() 'beneficio anual
Dim i As Integer, j As Integer, k As Integer, m As Integer
Dim sum As Double 'contador de beneficios anuales
m = InputBox("Indique el numero de simulaciones", "Numero de simulaciones", 1000)
Range("J3").Select
Range(Selection, Selection.End(xlDown)).ClearContents
Randomize
For k = 1 To m 'numero de simulaciones (anuales)
For i = 1 To 250 'recorre días del año
For j = 1 To Cells(i + 2, "H") 'recorre compras diarias
sum = sum + Application.WorksheetFunction.LogInv(Rnd, LN(1000), 0.01)
'cuenta beneficios por cada venta
Next j
Next i
Cells(k + 2, "J") = sum 'pone beneficios diarios en la matriz anual
sum = 0
Next k
End Sub
Function LN(x)
LN = Log(x) / Log(Exp(1))
End Function



Estaba buscando algunas referencias y lo que publicas e muy, muy bueno.
ResponderEliminarSalu2.
Este comentario ha sido eliminado por el autor.
ResponderEliminarJusto lo que necesitaba
ResponderEliminarTienen una plantilla que se pueda aplicarse al futb9l
ResponderEliminar